Biological intelligence rests on many learning abilities that artificial systems lack. Humans build expertise from the ground-up, acquiring knowledge that can be communicated and extended, updating their models of the world, and growing new concepts on those built previously to become better and faster learners the more we master a domain. This allows the acquisition of a potentially endless range of skills, like driving, cooking or writing poems. Meanwhile, machines can 'learn' to handle only a single class of problems at a time, because statistical ML models tend to interpolate (not extrapolate).

An important outcome of this is that while machine learning systems need tons of data to learn existing patterns, human learners can often generalize strongly from modest amounts of experience. The world's best chess-playing machine has to play millions of games to be able to match the average human grandmaster, who has played less than ten thousand games in her lifetime.

Yet current benchmarks for evaluating machine intelligence only measure task-specific performance - how well does it do at X? - and do not capture this disparity in generalization power. A more suitable way to compare intelligent systems would be to calculate the efficiency with which they are able to convert previous knowledge and experience into performance on a new task.  To build machines that can program themselves to do any task, you need to first measure how well they learn to do things they were never programmed to do.

Today we release a new benchmark that is the first attempt to precisely compute this. We call it the generalization index, or the g-index, for easy recall. It's designed to work across domains - from toy environments, to a wide range of real-world tasks.

  1. Paper : https://arxiv.org/abs/2109.12075
  2. Benchmark : https://github.com/mayahq/g-index-benchmark
  3. Toy Environment : https://github.com/mayahq/flatland
Figure 1 : (From top-left, clockwise) Program workflows generated to 1. Open browser tab, search for and play a video on Youtube. 2. Search for a given query in a browser using Google Search, scrape the results and save them to a file. 3. Show a dashboard for controlling an Industrial IOT setup and 4. Remotely control a drone using MQTT messages

Setting it up

Humans think in series of instructions - the machine equivalent for this is a program. The g-index formulation treats learning a new task as generating (or inducing) the correct program to solve it. Why program induction? The two representations of the same image information in Figure 2 below illustrate why it's useful. The pixel representation is a 256 x 256 array of zeros and ones, denoting white and black pixels. Meanwhile, the program representation is a set of instructions on how to draw that image using custom programs made by combining three kinds of functions - Line(), Rectangle() and Circle().

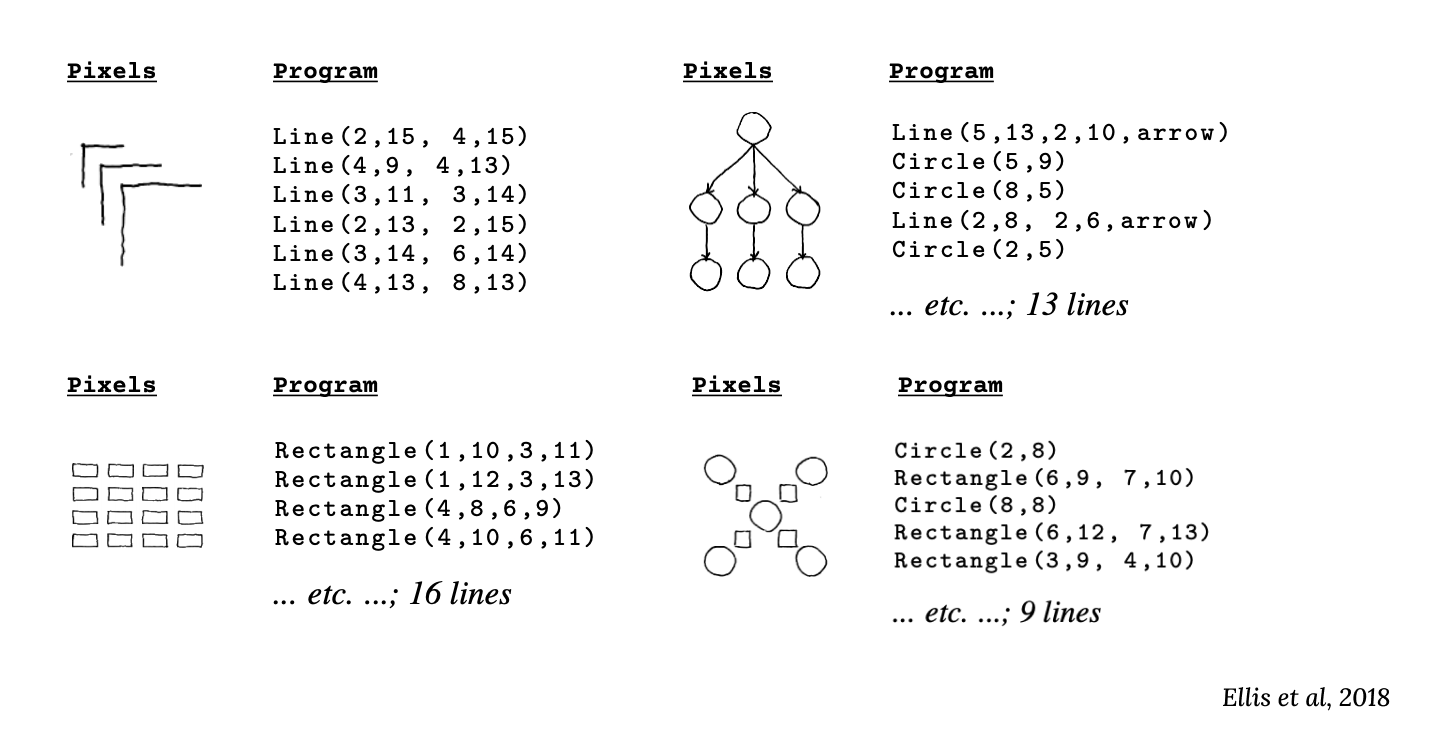
Figure 2 : Pixel vs Program representations of the same image.

It would require thousands of samples for today's machine learning systems to pick up patterns in the dense pixel representation. Meanwhile, the program representation is much easier to learn because it compresses the useful information into a few logic blocks, exposing knowledge that can be reused and composed to then generalize to increasingly more complex tasks.

Program representations are also easier for humans to study and interpret. For instance, when describing a giraffe, you inevitably enumerate the program that makes up the giraffe - "a tiny head on top of a long neck connected to a horse-like torso with four legs." Similar compositional programs span the entirety of human knowledge - from representing the structures of molecules, to the motions of planets. Sample efficiency and human interpretability are desirable qualities to build into thinking machines.

That said, program learning is highly sensitive to the choice of initial program syntax.  For instance, it would be hard to represent a spiral pattern (🌀), using just the functions Line(), Rectangle() and Circle() . Previous attempts to learn programs have found it essential to start with a carefully engineered domain-specific language (DSL), without which the programs to be discovered would be prohibitively long, and too hard to discover in reasonable search times.

To arrive at a measure of generalization power, the right choice of DSL should act as a common lingua franca to express and compare programs of real-world utility across a wide variety of domains. It would allow for a general-purpose way to :

  1. Express the shortest solution program to tasks of arbitrary complexity across domains.
  2. Score performance on any real-world task without needing to run the program, by calculating how similar the generated program is to the optimal solution.
  3. Compute the generalization difficulty of any new task, or how dissimilar it is from the system’s prior knowledge and experience.

The Factory Model of Programming

The flow-based programming (FBP) model of structuring programs as "data processing factories" comes the closest to ticking these boxes. Flow-based programs are defined as networks of reusable components running "black-box" processes, which communicate via data chunks (called information packets) travelling across predefined connections (think "conveyor belts").

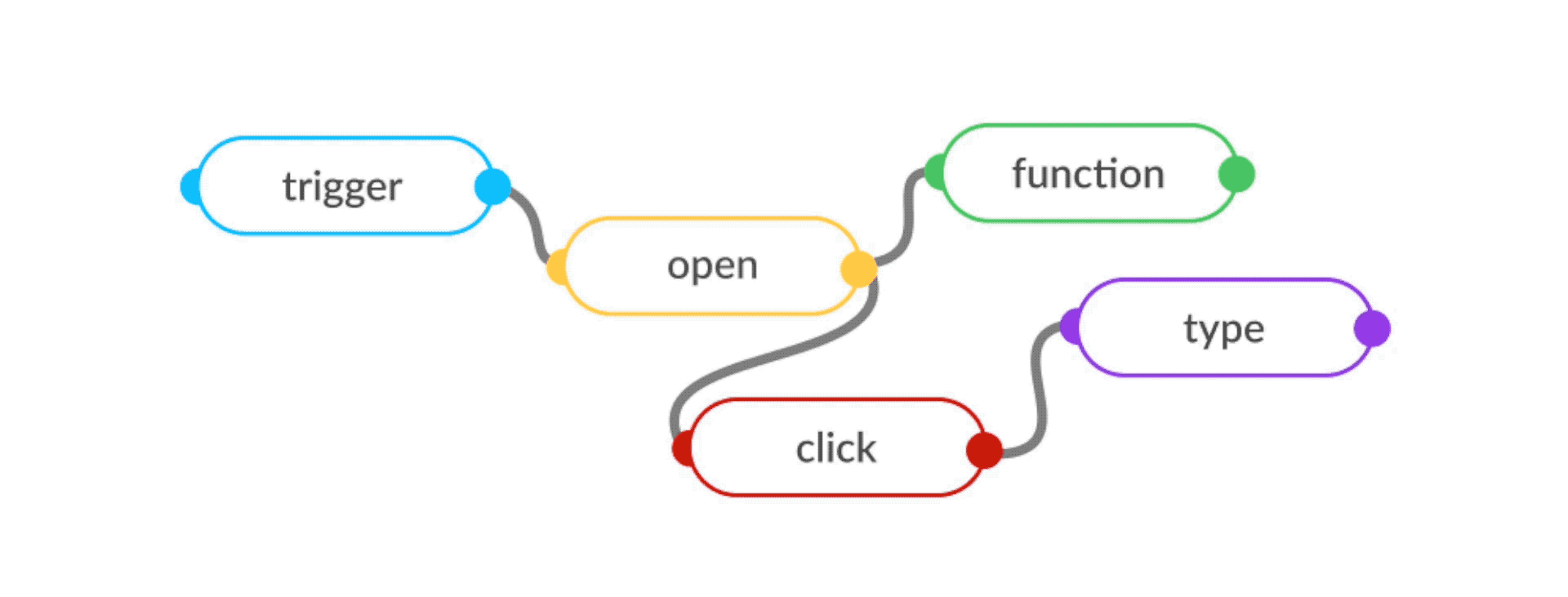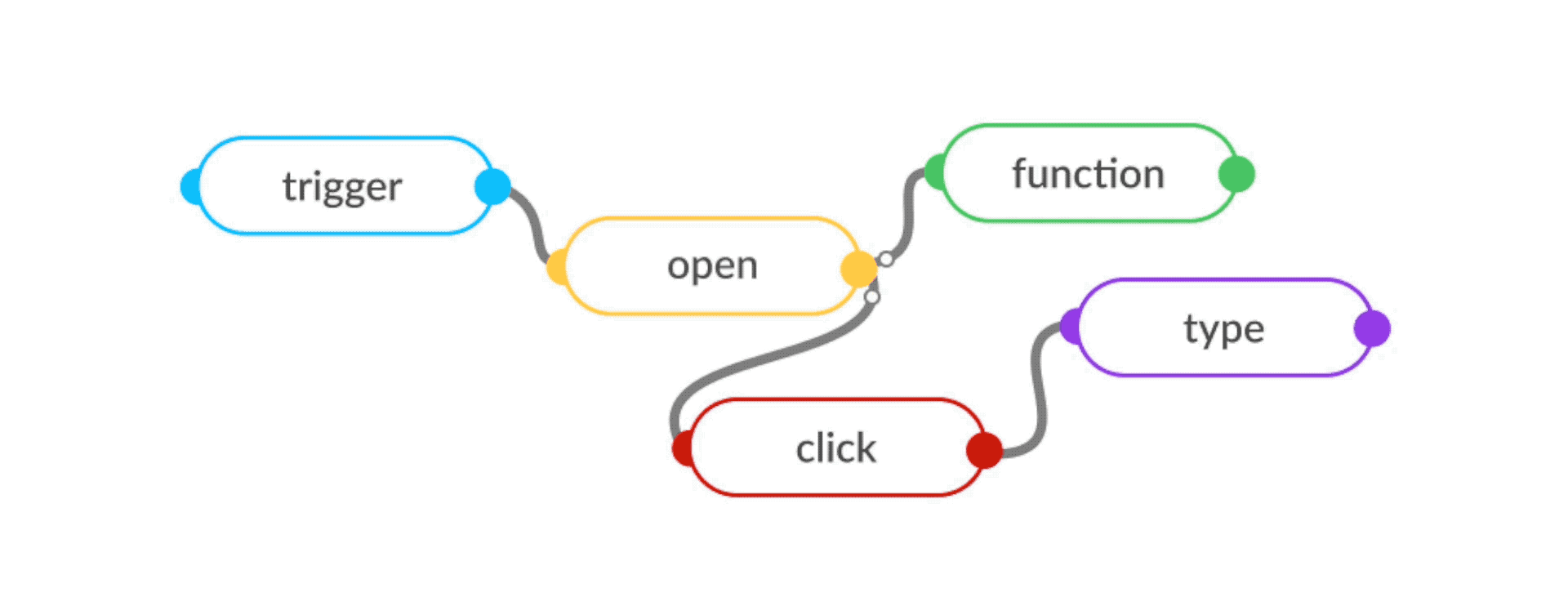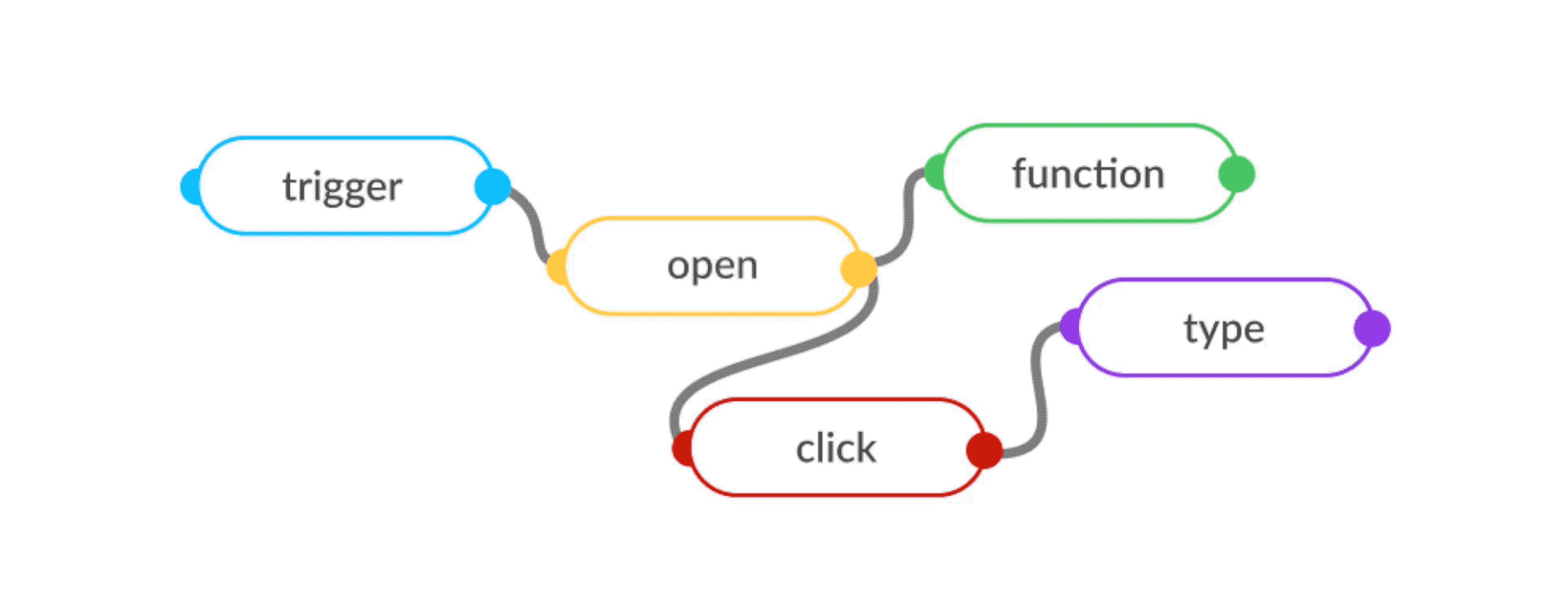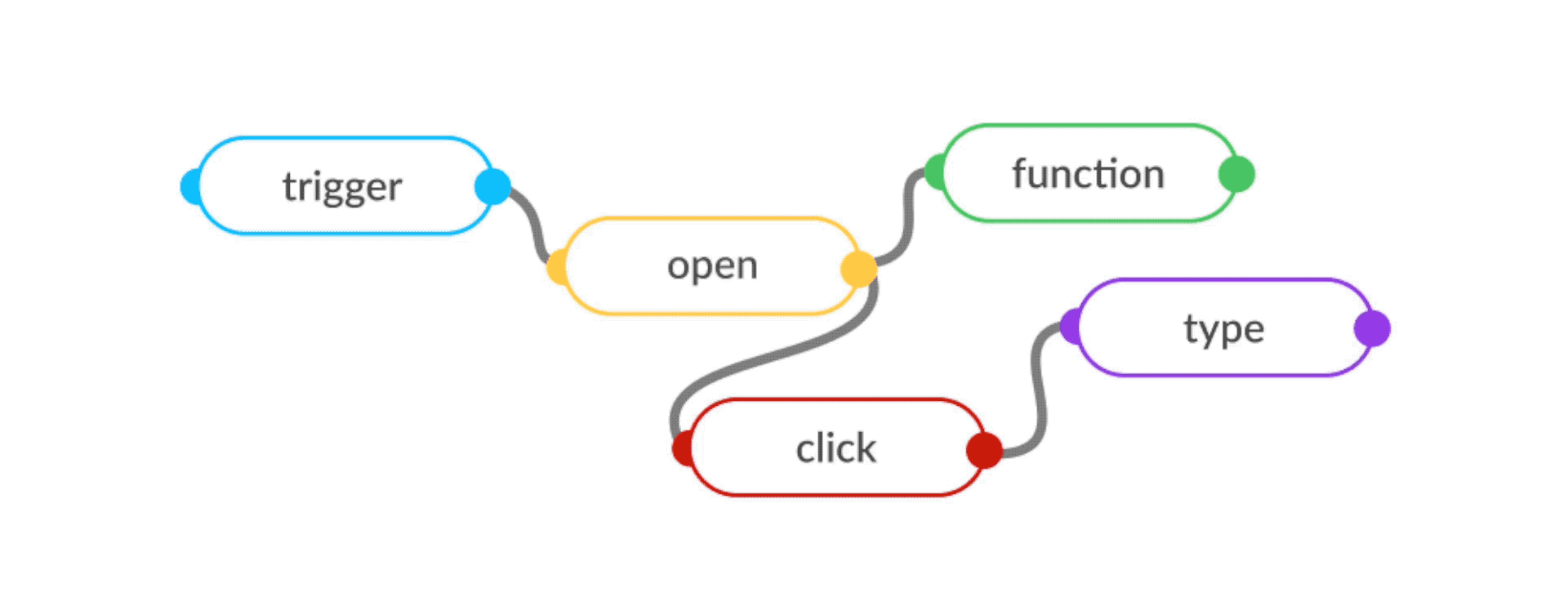
Figure 3 : Thinking of programs as factories

Reusable

FBP systems are easy to extend, modify and reuse without knowing about the rest of the program. The functional factory model allows the bundling of low-level components into higher-order "subflows", which can be then be reused as components for more complex tasks. This opens up ways to create human-like learners that grow new concepts on top of already-built knowledge.

Composable

FBP exhibits "data coupling", which is the loosest type of coupling between components. This means that the flow-based program that is learnt is merely the "coordination logic" to select and assemble these components in various combinations to solve a new task. The underlying "black box" logic for the components is language-independent and can be implemented using any framework, language, API, or combinations of other components.

Interpretable

FBP promotes a high-level, functional style of specifications that simplifies reasoning about program behaviour. The visual representations allow humans to quickly interpret these programs, while the graph structure allows algorithms to easily analyze them as discrete networks.

Expressive

Strong generalization comes from being able to do more with less. Similar to how a few dictionary words can be rearranged to make millions of English sentences, a few of these reusable FBP components can be wired together in different ways to do millions of different tasks across domains.

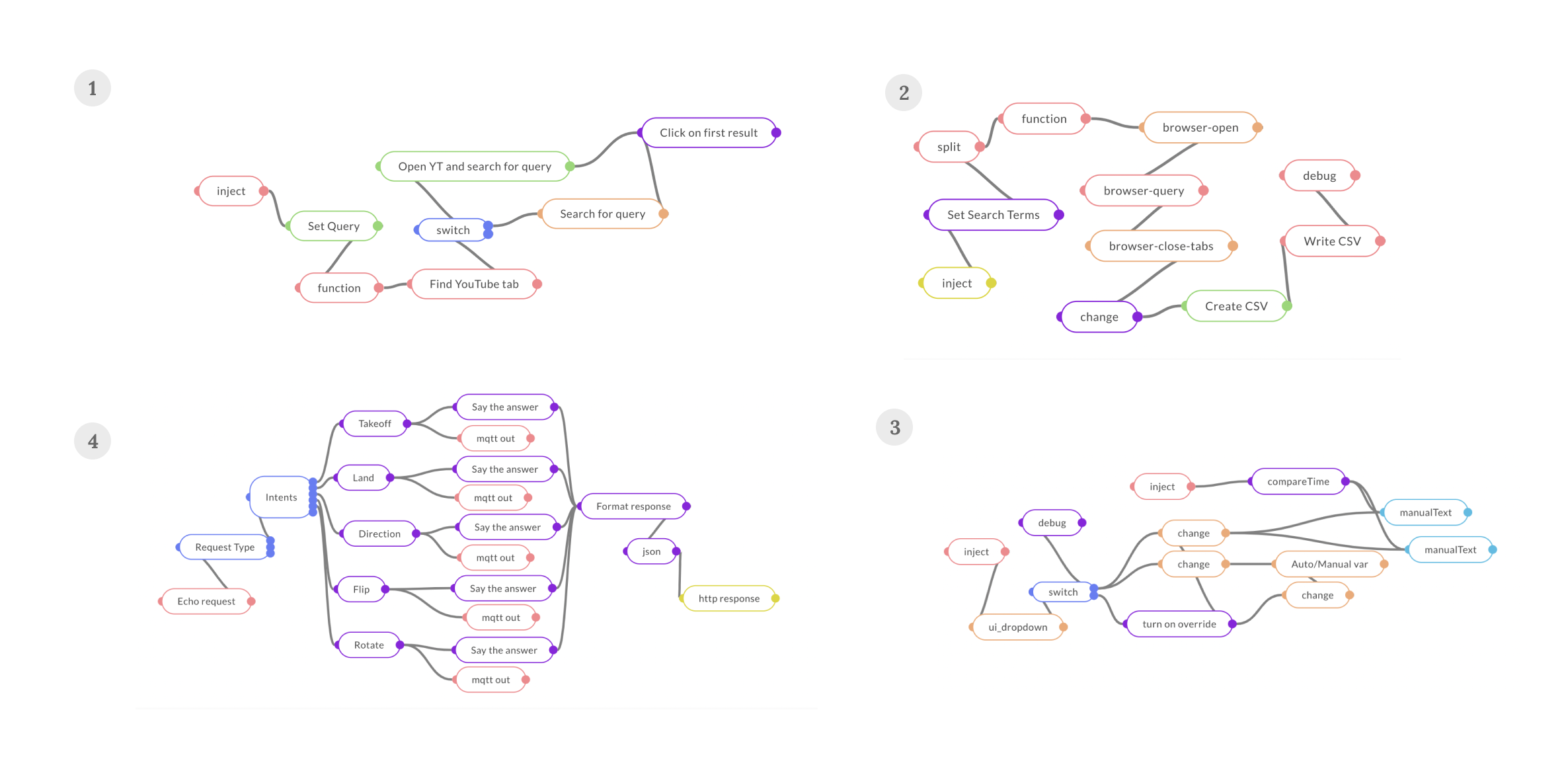
For demonstration, we introduce MayaLang, a custom flow-based language with components to do a wide range of tasks from navigating the web, to controlling drones (Fig 1). Fig 3 shows a sample of what a MayaLang program looks like in the form of a JSON array - a network graph with multiple nodes exhibiting different functions connected to other nodes via wires. To the keen observer, flow-based programs are simply functional programs, expressed in the form of directed acyclic graphs (more details in Section 2.3.1 of the paper).

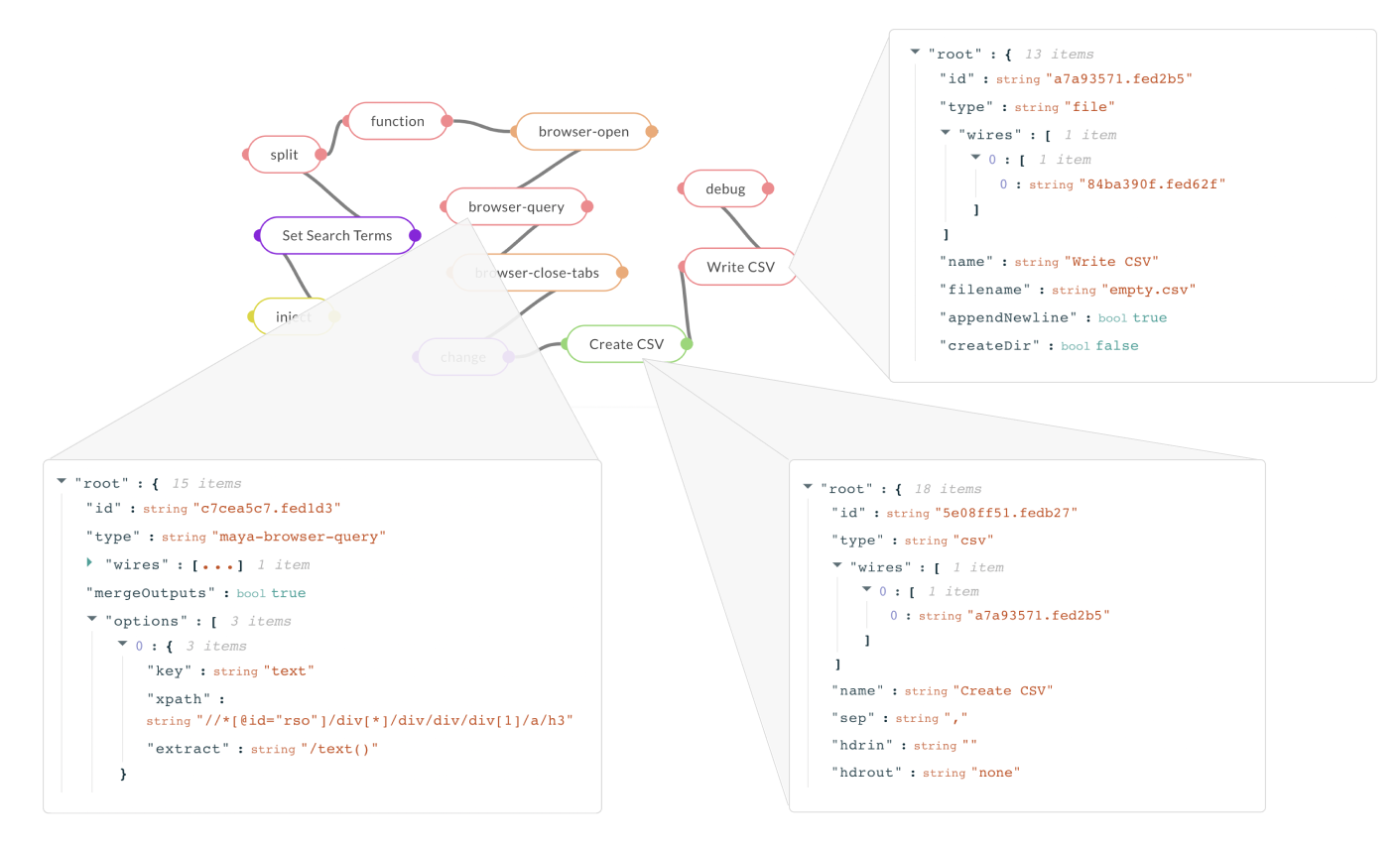
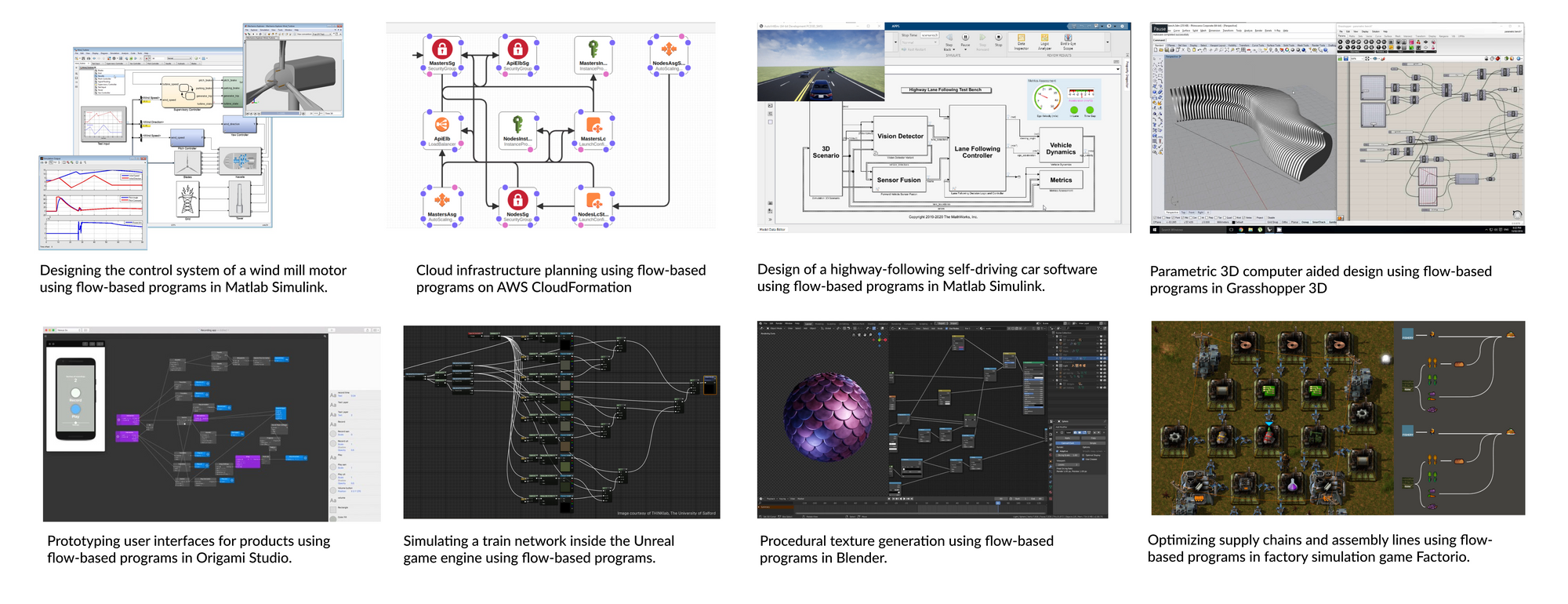
Figure 4: Representing a flow-based program as a directed acyclic graph in MayaLang - The JSON descriptions of three nodes are displayed - each node instance has unique id for reference and wires connecting it to other nodes. For the maya-browser-query type node, the attributes include mergeOutputs and options. The csv type node has a wire connecting it to the file node via its unique id.

While these are meant to run on MayaOS runtimes (a fork of the Node-RED engine), the methods used to learn them could be extended to any domain or execution environment. For instance, we introduce Flatland in our paper, a simple toy environment with the goal of inferring the right flow-based program to draw shapes in a 2D plane. On the other hand, Figure 4 below shows how the same flow-based programs can be used to solve a wide variety of complex tasks, from modelling control systems and setting up cloud infrastructure, to building CAD models and optimizing assembly lines.

Since they simply describe the coordination logic to link components, flow-based programs can be used to wire processes of any degree of complexity and of any functional behaviour together.  To teach machines how to understand and generate flow-based programs would open them up to a whole new world of creation.

Figure 5 : Developing methods to learning flow-based programs opens up a wide range of possible applications

Previous definitions of general intelligence rely on quantities like Kolmogorov complexity which are incomputable. Here, expressing solution programs as graphs provides us a second major advantage - since they are made up of symbols arranged in discrete ways, they can be compared with each other to obtain a numeric score.

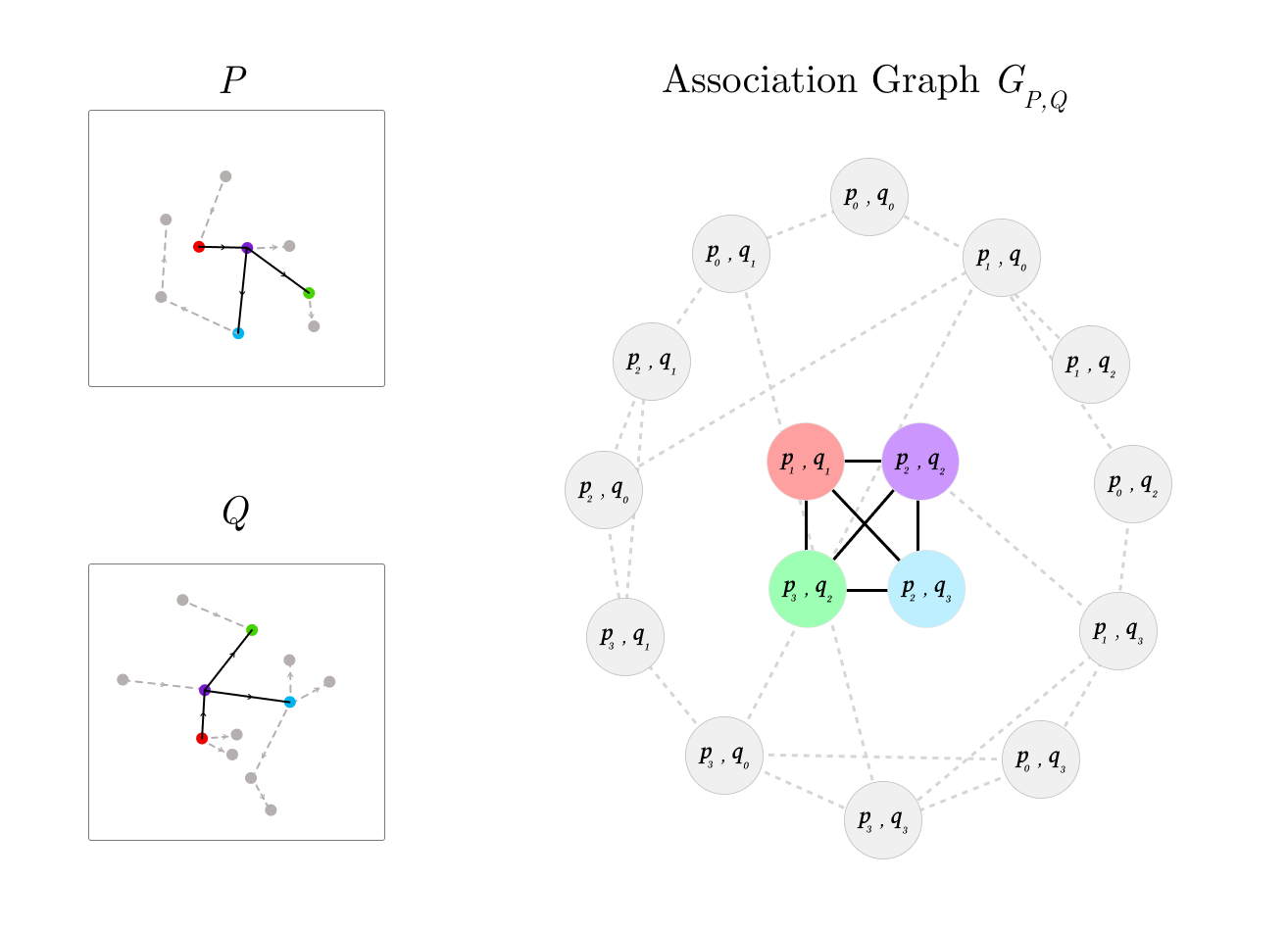
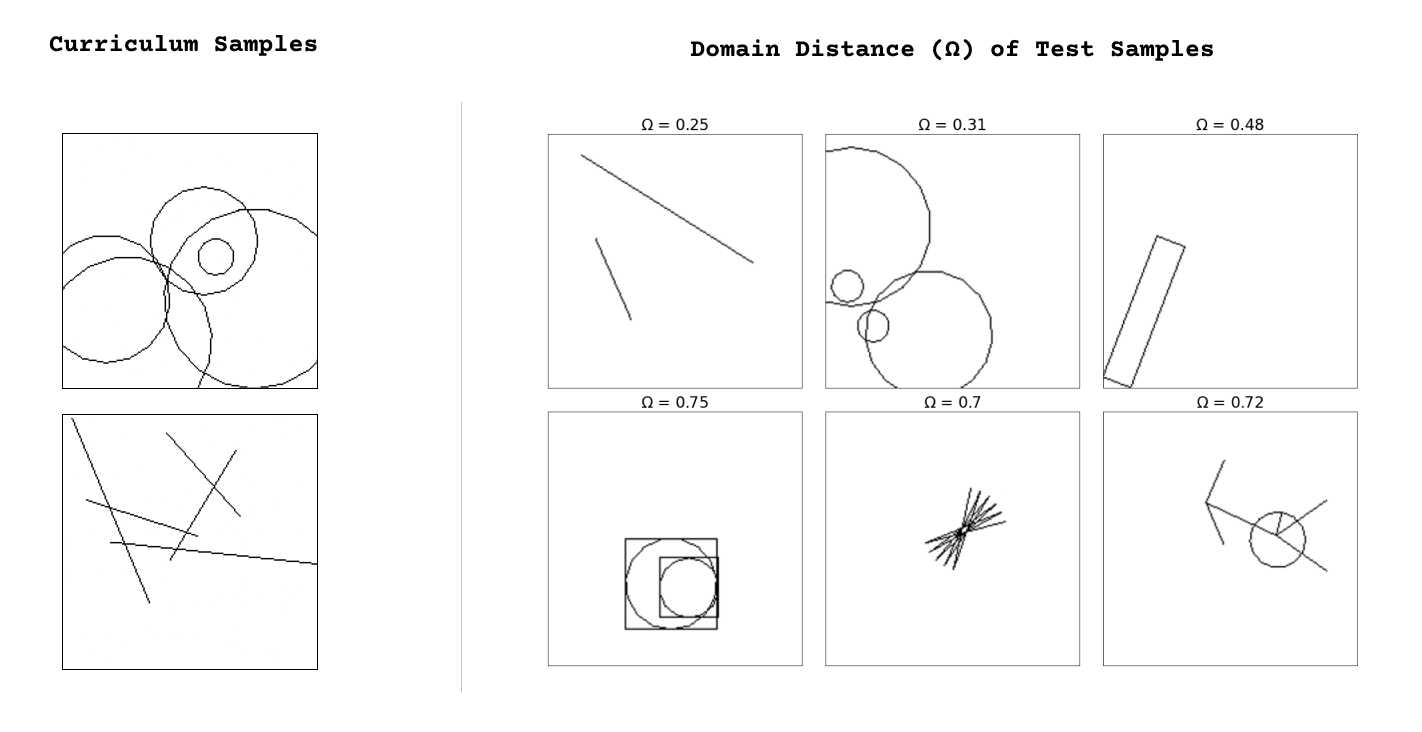
Figure 6 : We use subgraph isomorphism to compare any two flow-based programs and calculate a distance score between 0 and 1.

This allows us to compute the generalization difficulty of a new task, by measuring how dissimilar it is from a system's prior knowledge and experience (distance metric in Figure 7) . Similar comparison methods can be used to score task performance, by directly comparing the generated program with a known solution program. Refer to Section 2.4 of the paper for more details.

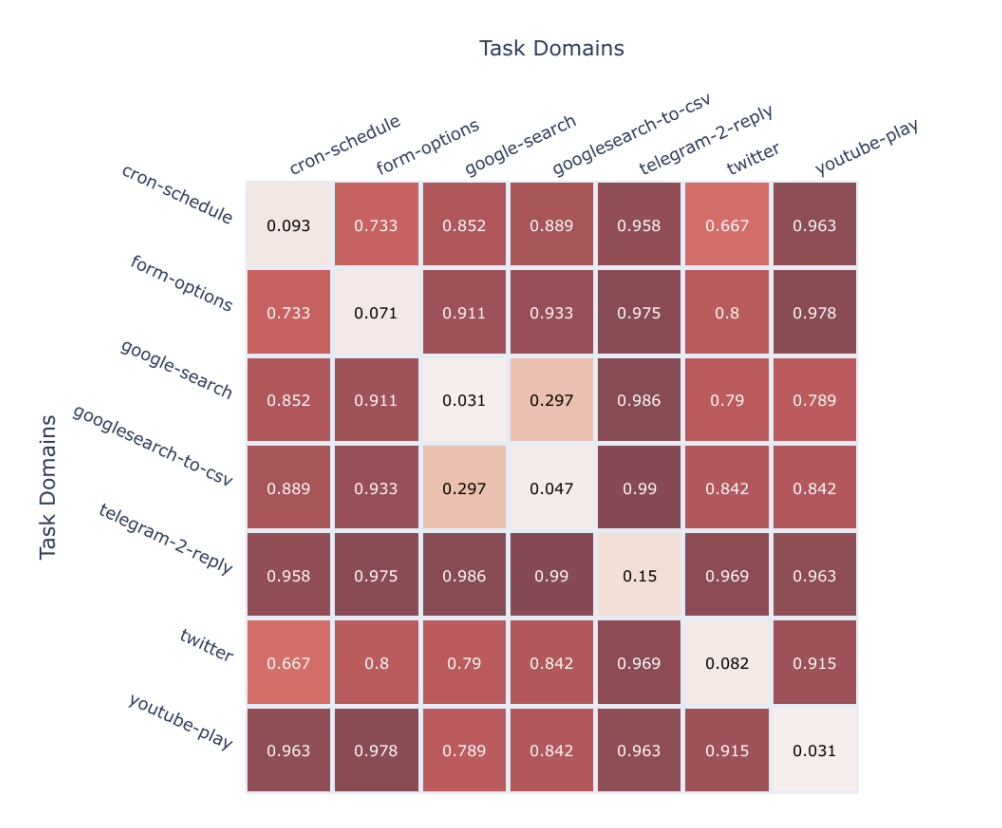
Figure 7 : Scores of the distance metric between skill programs across seven different task domains: cron-schedule, form-options, google-search, googlesearch-to-csv, telegram-2-reply, twitter, and youtube-play. Skill programs within the same domain have scores closer to 0, and those from different domains have scores closer to 1. A description of task domains is given in Appendix A of our paper.

Bringing it all together

We now have the components to build up the g-index :

  1. Solution programs are expressed in a custom programming language that can be extended to construct new programs without additional syntax complexity, which streamlines collecting and augmenting data for the intelligence system.
  2. The scoring function does not require running the program to compute the score, which means it can also be used as a loss function or reward function for training the intelligence system.
  3. An intuitive formulation of generalization difficulty based on nearest neighbours that reuses the scoring function.

We use a set of tasks  \(\{T'_1, T'_2, ...~T'_j,~...\}\) to evaluate an intelligence system \(IS\) trained on a curriculum \(C\) consisting of items \(C_i\). The task contribution \(TC\) of a single task to the g-index is made up by the performance \(\theta\) of the \(IS\) on the task, the task's generalization difficulty \(GD\), the priors \(\rho\), and the experience \(E\).  These components are calculated and combined into a single computable metric, the g-index :

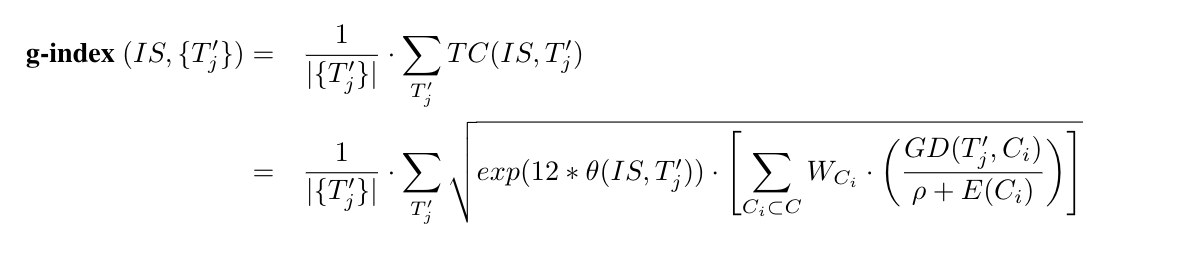
By design, the g-index exponentially rewards task performance \(\theta\) and generalization difficulty \(GD\), while penalizing data (\(W_{C_i}\) is a ratio that decreases as training samples \(C\) increase), compute \(E\) and initial prior knowledge \(\rho\).

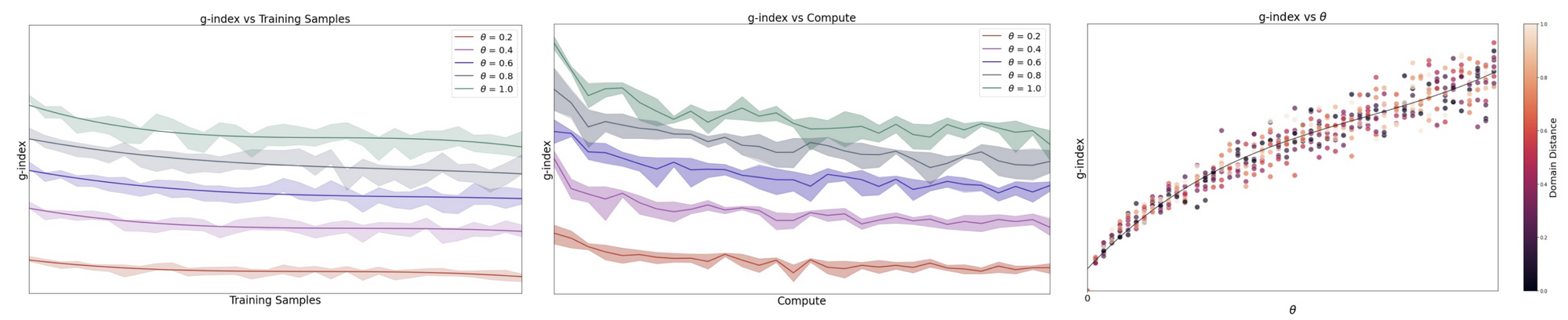
Figure 8 : How the g-index responds to changes in training samples, compute and performance (θ).

We fine-tuned large language models to produce flow-based programs in response to natural language descriptions, Table 1 contains their g-index scores. Note that the system with the best performance θ is not the one with the highest g-index , and the system with the worst θ score does not have the lowest g-index . The differences between the top three rows indicate the tradeoffs involved : while row 3 has better performance with less compute, the increased performance does not offset the penalty of double the number of training samples (refer to Section 4 of the paper for experiment details).

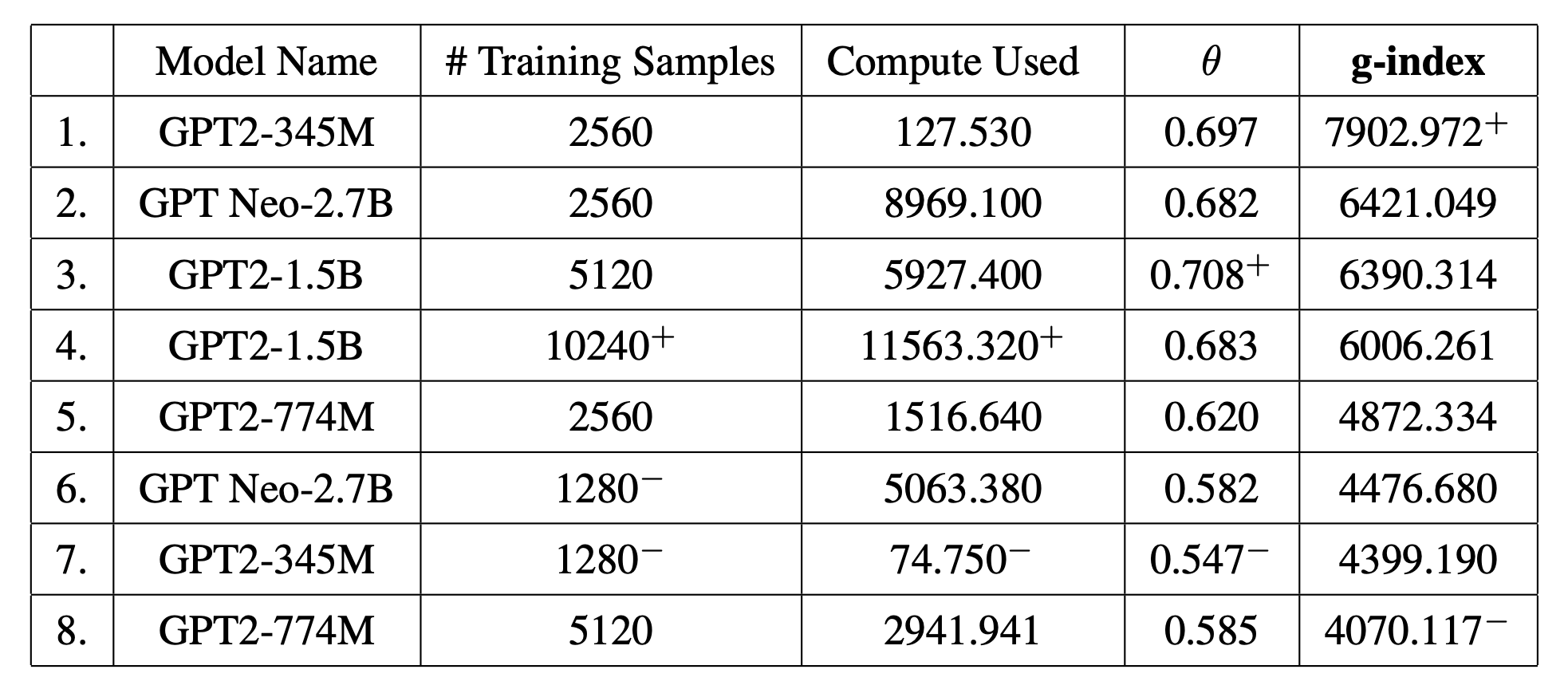
Table 1 : The best 8 performing models sorted according to their g-index scores. + indicates the column maximum, and − indicates the column minimum. More details in Section 4 of the paper.

The most 'general' models of today max out at the 7000-8000 range (regardless of their scale). A hypothetical self-improving digital superintelligence would clock a very high g-index of 60,000+. There's still a long way to go.

A quantitative benchmark like this allows us to measure and compare the relative generalization capabilities of different intelligence systems, and demarcate broad levels of generalization (similar to levels of autonomy for self-driving cars) to aid subjective discussions about the strengths and weaknesses of different approaches to build intelligence systems.

Levels of generalization

The g-index makes clear that general intelligence is not a binary property that a system either possesses or lacks, but is better described as a continuous spectrum . Where an intelligence system lies on this spectrum depends on the following factors of the evaluation setup:

  1. The diversity of the evaluation scope of tasks T - whether or not they lie within the similar domains where all tasks have low distance score relative to each other.
  2. The generalization difficulty of the task scope T with respect to its curriculum CC, or how different the tasks in the test scope are from the curriculum it has seen. (or the distance score).
  3. The efficiency with which a system converts its priors, experience with curriculum CC to a high performance on the task scope T

There are broadly four levels of generalization power based on the properties considered above. Each is harder to achieve than the previous one, and the formulation of the g-index makes it hard to brute-force a higher score by buying unlimited amounts of priors, data and compute.

Level 0 - No generalization

A L0 system encounters zero uncertainty in the tasks on which it is evaluated. This is because all edge cases are handled internally via hard-coded rules and the system does not act upon any learned heuristic. For example, a sorting algorithm, or a chess playing algorithm that iterates through all possible moves to decide it's next move.

Level 1 : Generalization to known variables in known domains.

An L1 general intelligence is able to generalize across predictable amounts of uncertainty within a set of related tasks in the same domain. Consider a set of task specifications of the form “Buy X stock every Y hours”. The variables X and Y here are ‘known unknowns’. Only some node properties are varied - no new nodes and wires are added, hence the generalization difficulty is low. If an intelligence system trained only on programs with different combinations of X and Y , or tasks of the form “Buy TSLA stock every 10 hours” and “Every 20 hours, buy AAPL stock” is able to learn to generate the correct program for unknown combinations of X and Y , then it can be said to have reached L1 generalization. Current deep learning-based approaches are reasonably successful at attaining this degree of generalization power.

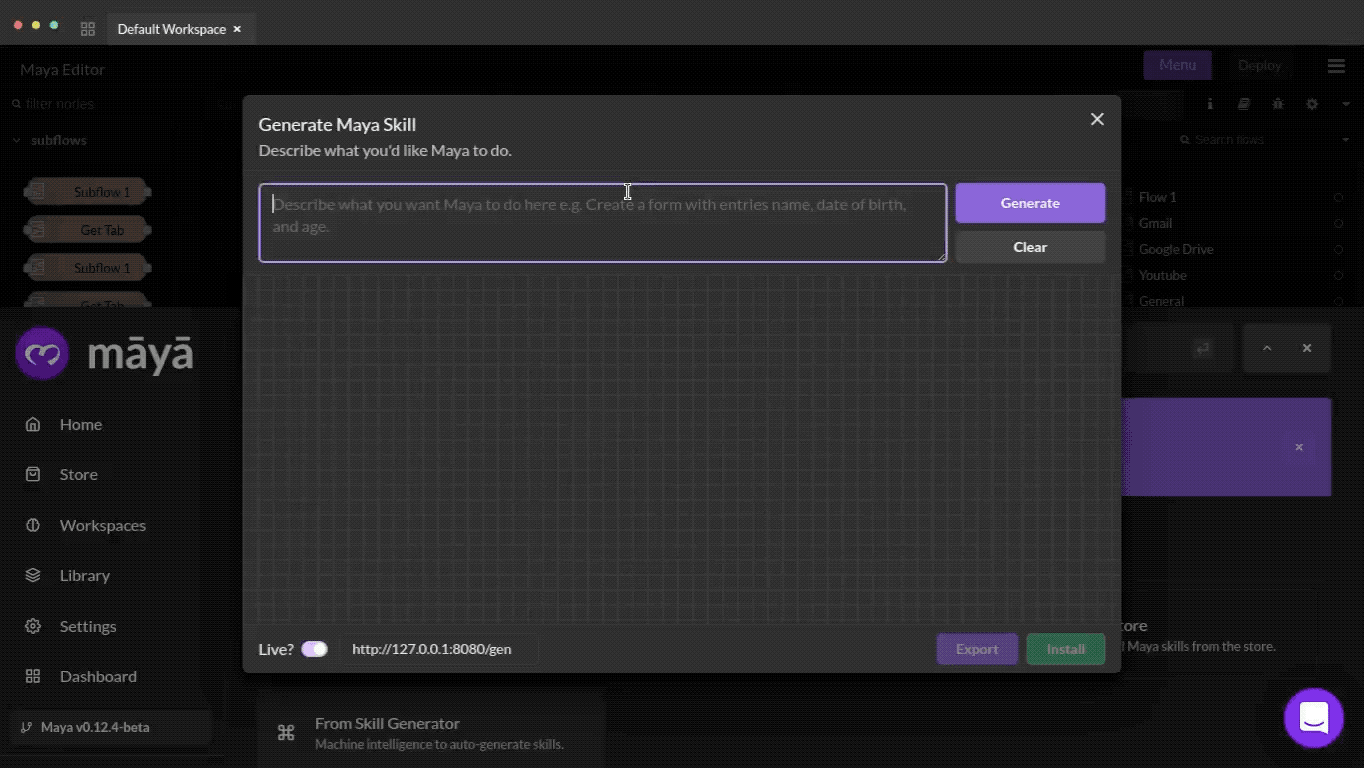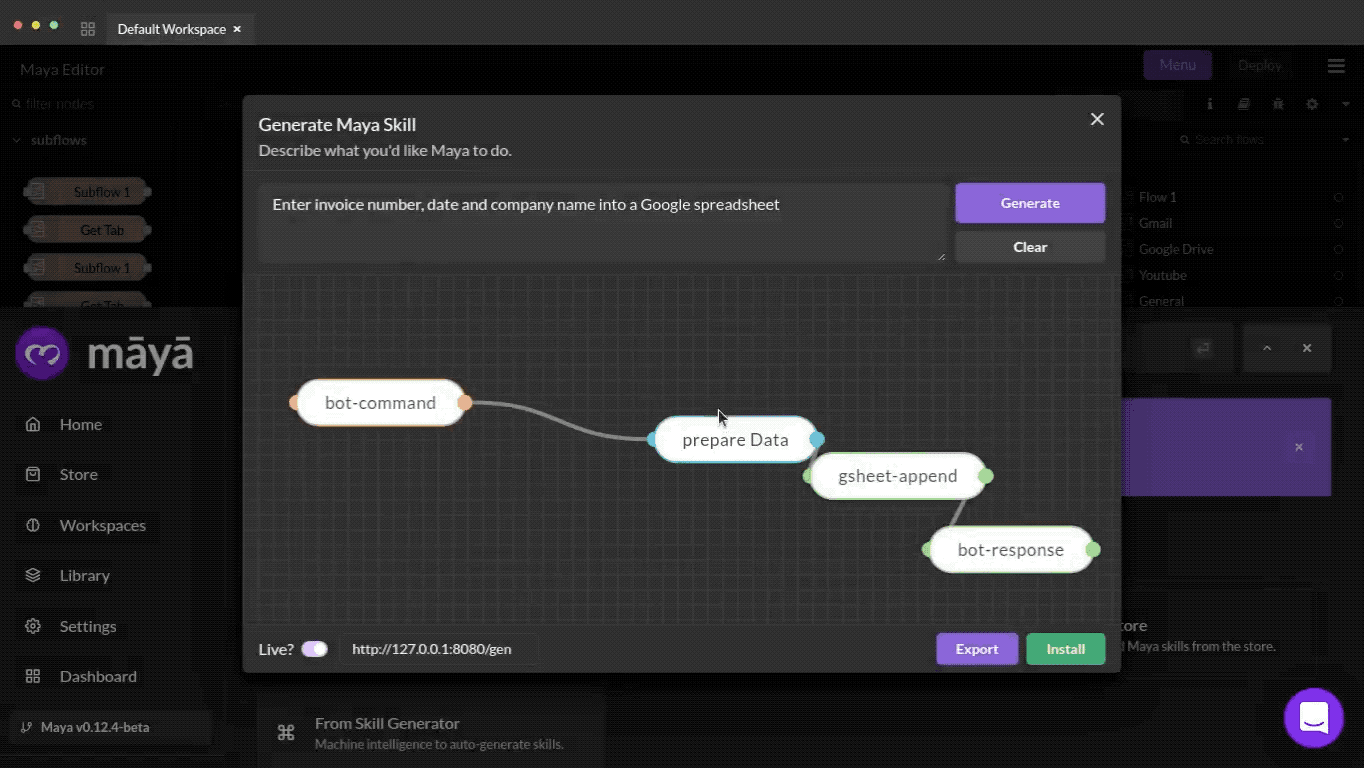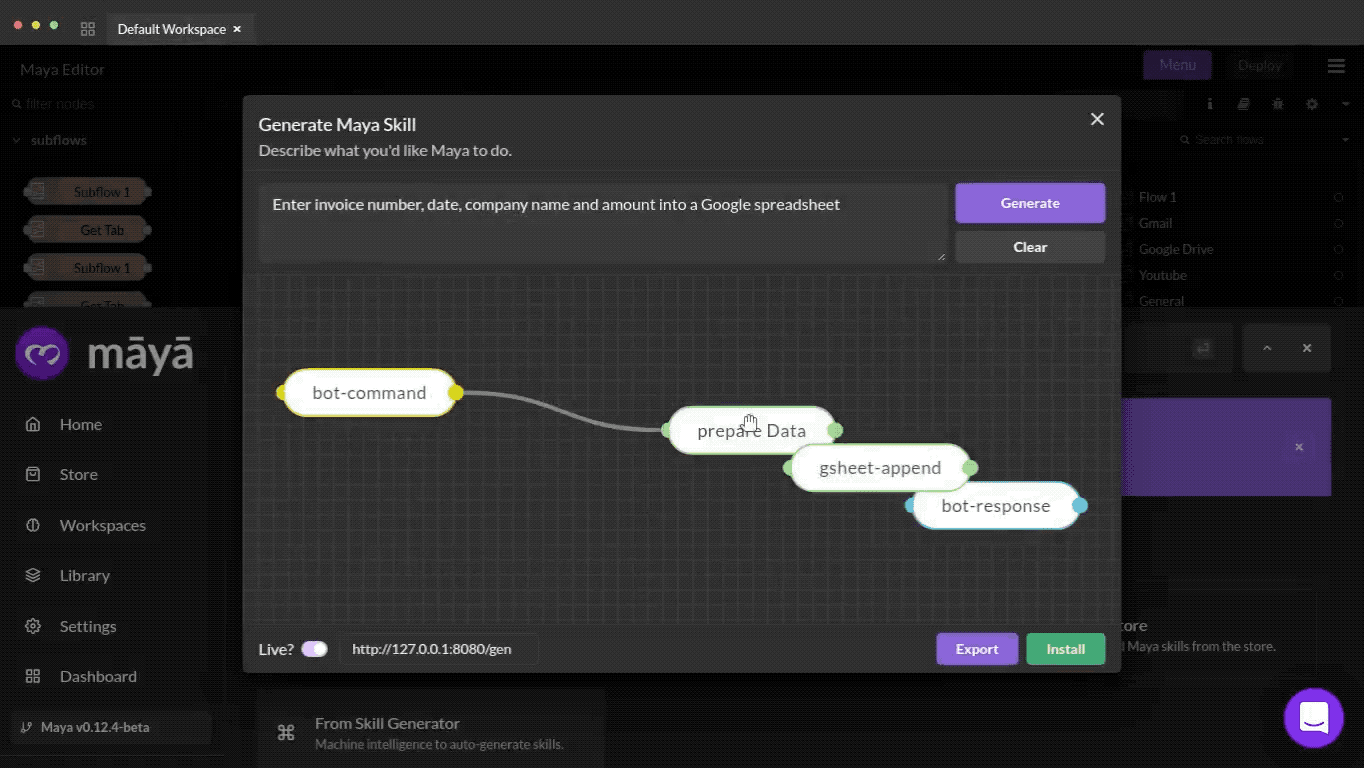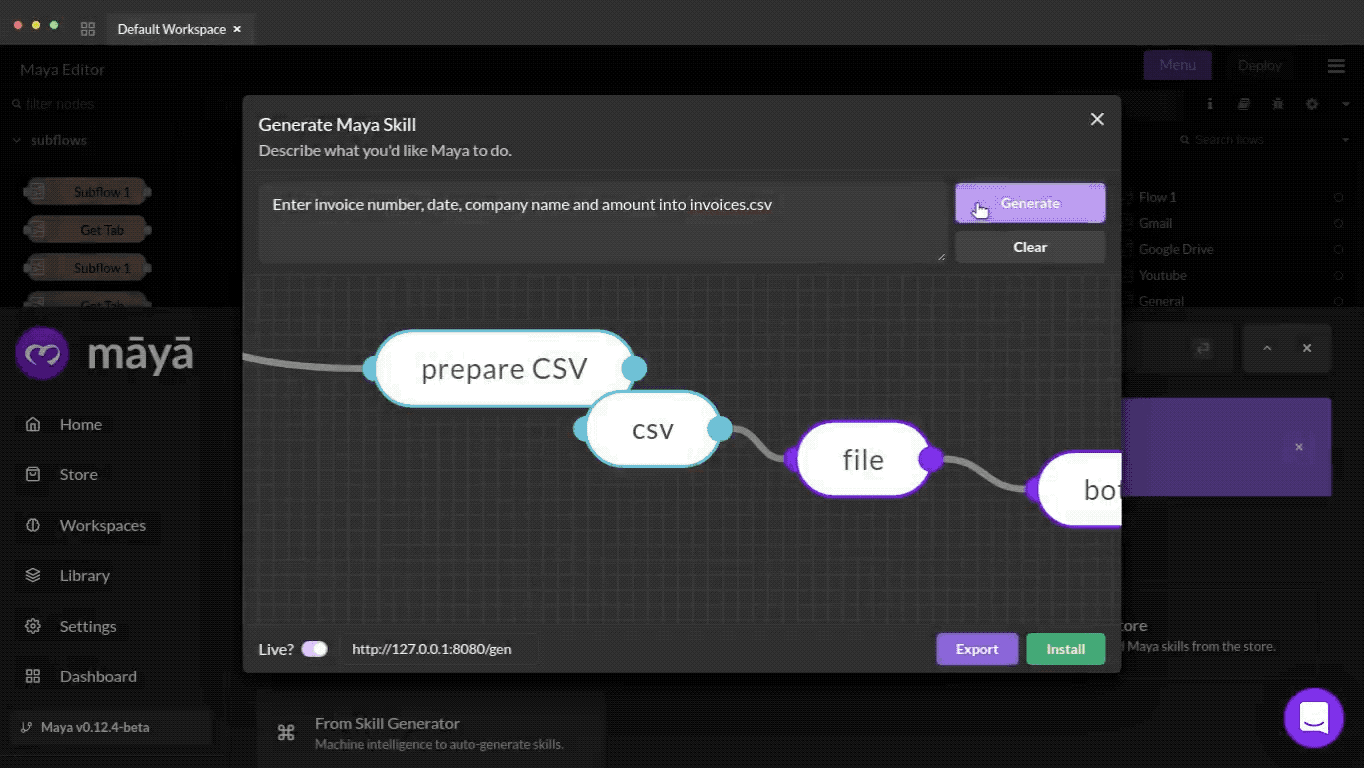
L1 generalization within the domain of automating data entry.

Level 2 : Generalization to unknown variables within known domains

An L2 intelligence system is able to generalize to unknown amounts of uncertainty, but within similar task domains. For example, when an intelligence system which has been shown in it’s training curriculum two different programs for the task specifications “Search for query on Google”, and another to “Save a list of items to file” is able to successfully generate a program solution for the new task specification T 0 : “Search for a query on Google and save results to file”. This task has mid-range generalization difficulty because the system has to learn how to combine two different program it has seen before. Unlike L1, the uncertainty here is not just with the attributes of nodes, but also with the extra nodes and wires needed to solve the task. This sort of composite program synthesis within known domains can be said to be an outcome of L2 generalization. While some deep learning systems are occasionally able to demonstrate L2 generalization when exposed to large amounts of data and compute power, we expect that sample-efficient methods of reaching L2 that score high on the g-index will require entirely new approaches to the problem.

Level 3 : Generalization to unknown variables across unknown domains

An L3 intelligence system is able to adapt to arbitrary amounts of uncertainty in the tasks on which it is evaluated. This is the most challenging level of generalization because it requires the system to perform well on tasks with high generalization difficulty, i.e. the nodes and wire connections in the solution program required to solve a task are highly dissimilar to any task it has seen before in it’s training curriculum.

For example, if an intelligence system that is shown only web navigation tasks of the form “Summarize page from Wikipedia.com”, is asked to “Learn how to drive a Toyota on a given city street”, it has to find novel ways to convert its experience in one domain into mastery in another completely unknown domain. For instance, it could do this is by using its web navigation skills to watch an online city-driving video tutorial, create a web-based simulation sandbox of the street with virtual car controls, program new node types to interface with the controls on a real car, and then be able to generate a program to drive a car down a street.

Current learning methods are insufficiently equipped to create or scale up to such an L3 intelligence system. We expect new methods will need to emerge which incorporate high sample-efficiency, embodied agency, long-term memory and elements of self-improvement.

While we don't know what methods get us to L2 and L3, there now might be one way to find out - beating the g-index benchmark.

Flatland - a toy environment for the g-index

The benchmark can be adapted to smaller toy environments without much compromise. We propose a simpler testbed called Flatland (code) that requires the intelligence system to infer the correct program to draw the given shapes in a 2D plane. (Section 5 in the paper)

Figure 9 : An example task in flatland with associated program and JSON representation which is similar to the programs generated from real-world tasks (Figure 4).

The evaluation setup is identical to the one with MayaLang, and the g-index is similarly benchmarked.

Figure 10 : Samples from the one set of training and test data for Flatland. The training set consists of various images containing one to five circles or lines. Above each test sample we display its domain distance Ω from the training set.

The simpler program space and fewer data bottlenecks in the Flatland environment opens up possibilities to explore a wide range of hard problems. The hardest questions above involve reimagining 'AI models' as embodied machines, not just "brains-in-a-jar" :

  1. How much does the choice of initial primitives/priors affect generalization?
  2. How is g-index affected when choosing higher-order primitives over lower-order primitives?
  3. How much does task specification to the algorithm (images, text, video) affect how well it learns the program to solve the task?
  4. How can a machine be taught to build knowledge on top of what it has already learnt?
  5. How much and what new data points does it need to change its mind and create new pathways of reasoning?
  6. If the learning algorithm is the control center, what are the sensors and actuators for the intelligence system that let it interact with the world?
  7. Can we build systems that suggest what sort of extra data they might need to get a higher g-index?
  8. What role does the order in which it is shown data play and can a system improve incrementally over time?
  9. What are the minimum set of steps you need manually take for a quantum improvement in the g-index for a given intelligence system?
  10. How can these steps be automated so a system might self-improve?

It is possible to generate unlimited Flatland data across tasks of different generalization difficulty, but the g-index explicitly penalizes brute-force memorization, so more data will not lead to a higher g-index. Since what is being learnt is a coordination language to combine different primitives together, methods developed to beat the g-index using such toy environments could surface insights that could be adapted to generate programs for real-world flow-based programs (Figure 1).

Conclusion

While we don’t expect the definition of g-index to be complete, it anchors a previously abstract concept in a precise formulation made up of quantities that can be measured via reproducible experiments. The flow-based programming language we propose can act as a functional "link" language to express and compare programs of real-world utility across a wide variety of domains. The g-index explicitly rewards resource-efficiency, which we hope incentivises sustainable ways of achieving generalization which do not rely on unlimited amounts of compute and data.

A good outcome of this would be the patronage and competitive development of new methods and technologies to reach higher g-index levels, similar in spirit to the Hutter compression challenge. Intelligent machines will only be able to contribute to real technological progress when they can learn how do more from less, not the other way around. If we want to one day be able to build highly autonomous systems that learn quickly, improve themselves, solve hard problems and one day travel out, explore and colonize the uncharted swathes of space, we have to start with measuring precisely how well they adapt to the unknown.‌‌‌‌

  1. Paper : https://arxiv.org/abs/2109.12075
  2. Benchmark : https://github.com/mayahq/g-index-benchmark
  3. Toy Environment : https://github.com/mayahq/flatland

Bibliography :

  1. Page 24 of the paper.
  2. Acknowledgements : Thanks to François Chollet for his insights and feedback, and to Joshua Tenenbaum and Kevin Ellis for their program synthesis work.